Gauss
Carl Friedrich Gauss. Have you ever heard of him? He was a German mathematician from the early 1800’s. Considered to be one of the greatest mathematicians ever. Belongs on the Mount Rushmore of math geniuses, up there with Euclid, Newton, Einstein, and maybe your high school trigonometry teacher. Personal friends with Ludwig von Beethoven (maybe not, but they were Germans of right about the same age, although Beethoven had moved to Austria).
Why should an investor care about Gauss? Because he came up with The Bell Curve, also known as the Normal Distribution Curve. All of us have seen it:
There are several bodies of academic study at play here. You have Probability Theory, which addresses the likelihood of a random event actually occurring. You have Randomness, which, in the investment world, is the notion that investment returns are Random, and not a result of some reason or design. Burton Malkiel, an American economist and author who remains active today, wrote “A Random Walk Down Wall Street”, which made famous the notion that investment returns are random. Closely related is the Efficient Market Hypothesis, which posits that stock prices immediately reflect all available information, meaning that technical analysis and possibly fundamental analysis of individual stocks is futile. All of these may be future blog topics. Perhaps I can find an artist who can draw Gauss and Malkiel randomly walking hand-in-hand.
If investment returns are indeed Random, then they can be measured and graphed, and their graph would resemble the above Normal Distribution Curve. Then, taking the next step, one can use that curve (and its inherent mathematics) to predict (with perhaps 68% or 95% probability) that future returns will fall within a plus-or-minus range of percentages.
All of today’s algorithmic stock trading has its roots in Gauss’s work. You could say C.F. Gauss is the gross-gross-grossvater of algorithms. Gazillions of dollars, Euro, Yen, and other currencies are now at work under the assumption that Gauss was onto something.
But what if Gauss was wrong? What if future event outcomes do not look like past event outcomes? Gauss himself offered answers to this, with the concepts known as Skewness and Kurtosis. The following chart represents a Normal Distribution (red line), a Skewed Distribution (green line) and two Kurtotic Distributions (flat, or Platykurtic, which is the yellow line, and steep, or Leptokurtic, which is the blue line).
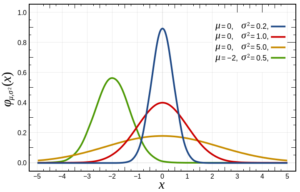
The green Skewed line shows that the bulk of the returns (or random events) are not concentrated around the Mean. The Platykurtic yellow line shows returns that are not as concentrated around the mean as in the Normal distribution, and the Leptokurtic blue line shows returns highly concentrated around the mean. So, Gauss had alternatives to the Normal state of things.
However, what none of these graphs show is a situation where many returns or events are far away from the Mean. In other words, none of these show “Fat Tail” or “Black Swan” events. The “tails” on these graphs are the extremes, at -5 or +5 standard deviations or even farther out on each extreme. Imagine investment returns which are 5 or more standard deviations from the Mean – the Black Monday 1987 crash comes to mind, as does the 2008 correction that occurred over a longer (but still short) period of time.
Notice that these “Fat Tail” events I cited are to the downside. There are numerous other examples in the world of individual stocks (i.e., Enron, and employees who lost everything there because all they owned was Enron stock). An old saying is that stocks take the stairs up to the top and the elevator down. So maybe the Distributions should have their right (or positive) leg close to the X axis but the left (negative) leg raised up a bit, maybe about to kill a bug on the ground?
IMO
I believe the Normal Distribution is a mostly but not fully accurate way of graphing investment returns and therefore a somewhat flawed way of predicting future returns. If it was fully accurate, Long Term Capital Management would still be around (if you don’t know about its collapse in 1998, Google it). I believe trading algorithms are very useful and have indeed made billionaires out of their best practitioners. However, I also believe in Fat Tail/Black Swan risk, and that an investor needs to have some form of protection in place to guard against these risks. Being diversified among asset classes, being liquid (i.e., able to sell quickly if Armageddon happens), and having a strong portfolio manager are all good forms of portfolio protection.
